南卓铜 ([email protected])
我之前介绍过这个ios上的小app,功能很强大。微信有朋友反映说用起来还是有点困难。的确是这样。昨天又碰到小朋友问一个动点问题,他们老师讲的她理解不透。
这个问题是:
【2014玄武一模】在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P.
- 如图1,当点O在AC上时,试说明2∠ACP = ∠B;
- 如图2,AC=8,BC=6,当点O在△ABC外部时,求CP 长的取值范围。
Sketches的工具里有画直角三角形(在N边形工具里),也有画圆的(三点画圆或圆心及圆弧上一点确定圆),所以我们可以很简单画出△ABC (图3)与⊙O(图4)。然而我们要求是⊙O切AB于P点。Sketches并没有这样的直接工具。即使我们手动拖动点O以移动⊙O,使之看起来与AB相切,但并不能生成一个相切点P (图5)。
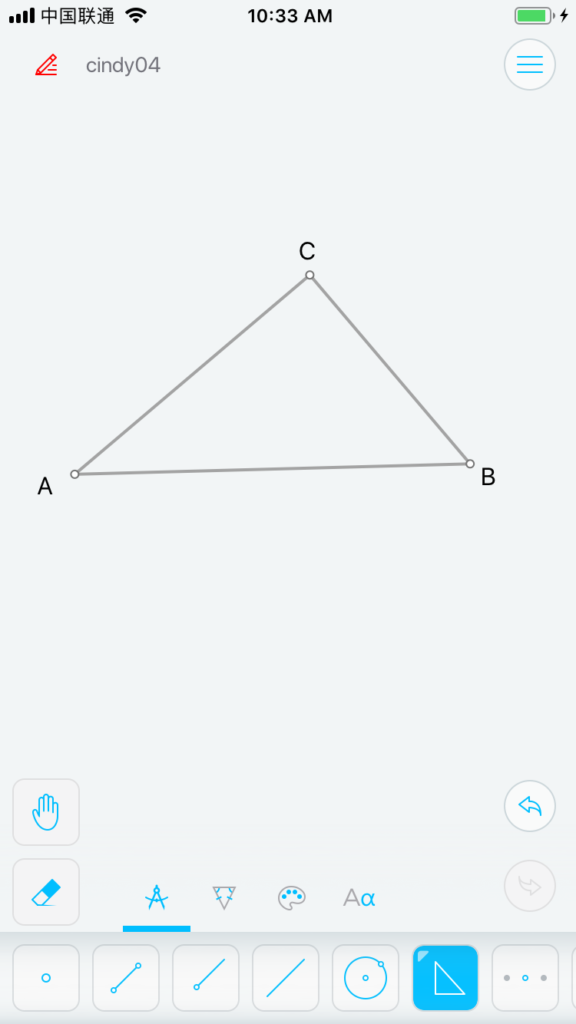
图 3 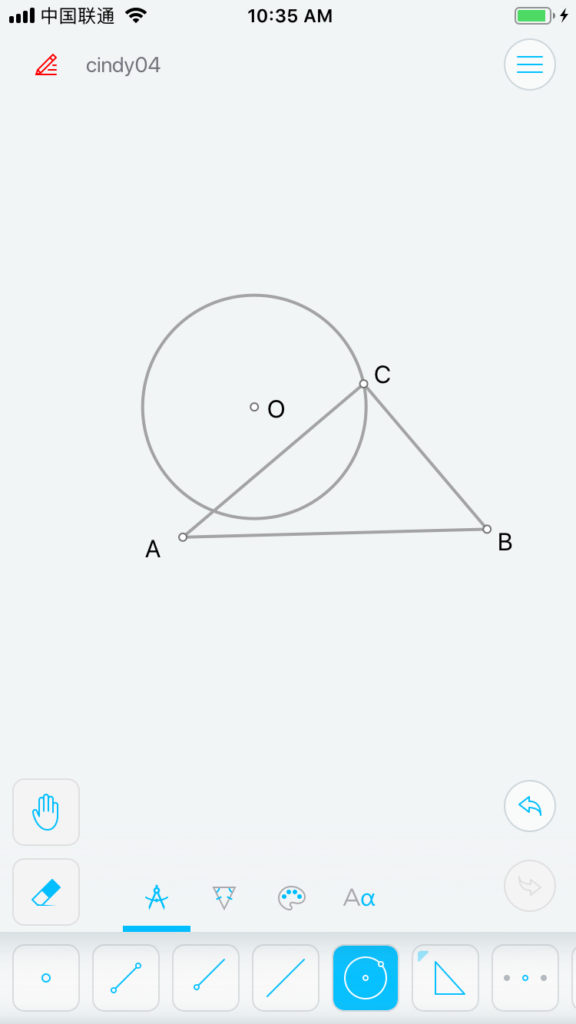
图 4 
图 5
这个问题是关注CP的取值范围,我们换一个思路,生成三角形后,先生成点P (图6),然后再想法子过C、P点生成⊙O。如果能生成,我们就可以拖着点P在AB上移动,观察CP的变化了。
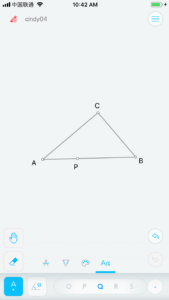
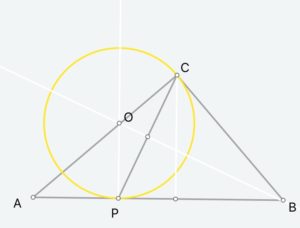
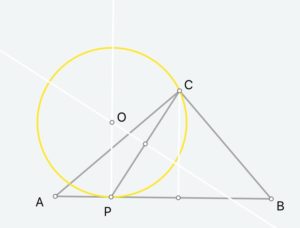
有这个思路后,生成⊙O就不难了,由于C、P在圆上,那么圆心必然过CP垂直平分线(图7);而由于圆要切于P,那么圆心也要垂直到AB,所以过P点可以再做垂线 (图8),相交点即圆心O。然后通过点O与C构造圆O (图9)。
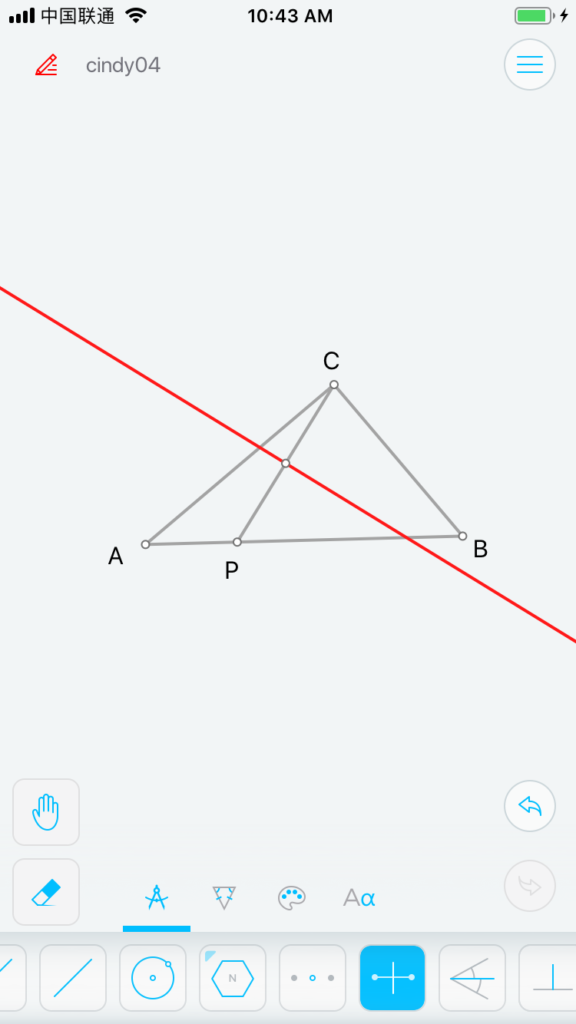
图 7 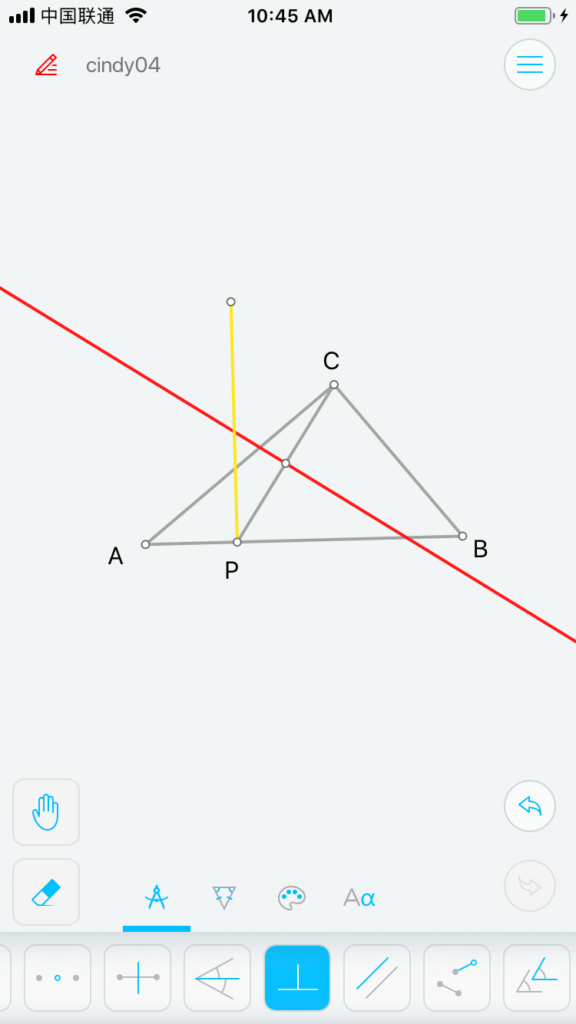
图 8 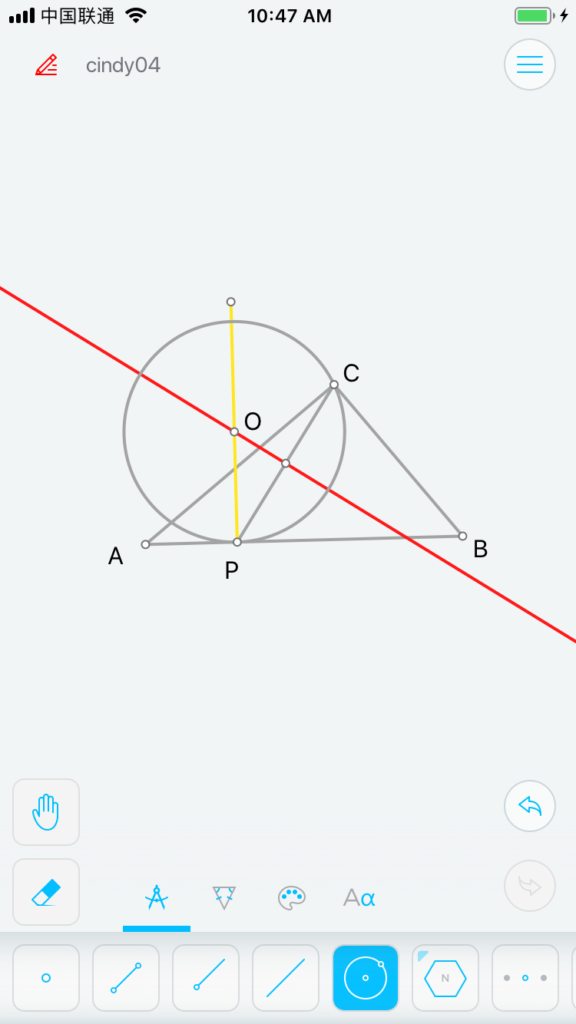
图 9
通过拖到点P在AB上移动 (动图/视频),我们就可以发现,圆心在三角形有两种情况,一种是在AC外,一种是在CB外。第一种情况时,P点移到A点重合时,CP最长(CP = AC);O点落到AC上时,CP最短;第二种情况时, P点移到B点重合时,CP最长 (CP = BC);O点落到CB上时,CP最短。综合分析下来,由于AC > BC,所以CP 最长的情况是等于AC,最短的情况是O点落在BC上时,需要求解这种情况时的CP (图10)。